Call & Put Options — Mechanics, Payoffs & Practical Examples

A clear, in-depth study of call and put options: payoff formulas, moneyness, breakeven, worked examples, practical uses (hedge, speculate, income), and an intro to Greeks.
This chapter provides a rigorous and detailed examination of the two foundational instruments in options trading: calls and puts. We will define them with precision, derive their core payoff formulas, and illustrate their mechanics with comprehensive numeric examples. Crucially, we will explore their practical applications for hedging, income generation, and speculation. The concept of the premium as the buyer's maximum loss and the seller's initial gain is paramount; study the examples carefully to internalize this fundamental risk-reward structure.
1. Foundational Definitions
- Call Option: A financial contract that grants the buyer the right, but not the obligation, to purchase a specified quantity of an underlying asset (e.g., shares, an index) at a predetermined price (the strike price) on or before a specified expiration date.
- Put Option: A financial contract that grants the buyer the right, but not the obligation, to sell a specified quantity of an underlying asset at a predetermined price (the strike price) on or before a specified expiration date.
- Buyer (Holder): The party that pays an upfront premium to acquire the rights (to buy or sell) conferred by the option contract. Their maximum potential loss is strictly limited to this premium amount.
- Seller (Writer): The party that receives the premium from the buyer. In exchange, they assume the obligation to fulfill the contract terms (to sell or buy the asset) if the buyer chooses to exercise their right. The seller's risk is typically much higher than the buyer's.
2. Core Payoff Formulas (At Expiry)
To quantitatively analyze option outcomes, we define the following variables:
S = Underlying asset's spot price at the moment of expiry
KP = Premium paid (for buyer) or received (for seller) per share
The max() function selects the higher of two values, ensuring payoffs are never negative.
- Long Call Payoff (Net Profit/Loss for the Buyer):
max(0, S − K) − P
Logic: The right to buy at K is only valuable if S > K. The profit is this value minus the initial cost. - Long Put Payoff (Net Profit/Loss for the Buyer):
max(0, K − S) − P
Logic: The right to sell at K is only valuable if S < K. The profit is this value minus the initial cost. - Short (Written) Call Payoff (Net Profit/Loss for the Seller):
−max(0, S − K) + P
Logic: The seller's payoff is the mirror image (opposite) of the buyer's payoff, plus the premium they collected. - Short (Written) Put Payoff (Net Profit/Loss for the Seller):
−max(0, K − S) + P
Logic: The seller's payoff is the mirror image (opposite) of the buyer's payoff, plus the premium they collected.
Intuition: A long call position profits when the underlying price rises significantly above the strike price. A long put position profits when the underlying price falls significantly below the strike price. The seller's perspective is always the inverse.
3. Moneyness: Defining an Option's Status
Moneyness describes the relationship between the current spot price (S) and the strike price (K), determining the immediate exercise value (intrinsic value) of the option.
- In the Money (ITM): The option has positive intrinsic value.
Call: S > K (e.g., Stock at ₹1,050, Call Strike ₹1,000)
Put: S < K (e.g., Stock at ₹950, Put Strike ₹1,000) - At the Money (ATM): S ≈ K. The option has no intrinsic value, only extrinsic (time) value.
- Out of the Money (OTM): The option has no intrinsic value.
Call: S < K (e.g., Stock at ₹950, Call Strike ₹1,000)
Put: S > K (e.g., Stock at ₹1,050, Put Strike ₹1,000)
4. Worked Numeric Examples with Scenarios
Assume a standard equity options lot size of 100 shares for these examples. Total P&L is calculated as (Per Share P&L * 100).
Example A — Long Call: Bullish Speculation
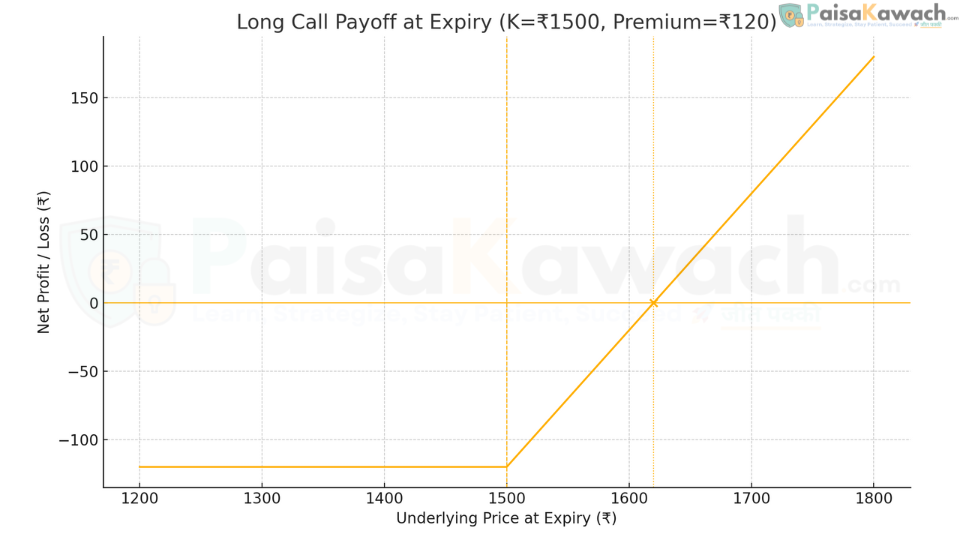
- Underlying: XYZ Stock
- Strike Price (K): ₹1,500 (~$18.00)
- Premium Paid (P): ₹120 (~$1.44) per share
- Total Cost: ₹120 * 100 = ₹12,000 (~$144) (Max Loss)
Scenario 1: Expiry at ₹1,650 (Bull Case)
Intrinsic Value = max(0, 1650 - 1500) = ₹150
Net Profit Per Share = ₹150 - ₹120 = ₹30 (~$0.36)
Total Net Profit = ₹30 * 100 = ₹3,000 (~$36)
Scenario 2: Expiry at ₹1,500 (Flat Case)
Intrinsic Value = max(0, 1500 - 1500) = ₹0
Net Loss Per Share = ₹0 - ₹120 = ₹120 (~$1.44) (Total Premium Lost)
Total Net Loss = ₹12,000 (~$144)
Scenario 3: Expiry at ₹1,400 (Bear Case)
Intrinsic Value = max(0, 1400 - 1500) = ₹0
Net Loss Per Share = ₹0 - ₹120 = ₹120 (~$1.44) (Total Premium Lost)
Total Net Loss = ₹12,000 (~$144)
Breakeven Point (BEP) = K + P = ₹1,500 + ₹120 = ₹1,620 (~$19.44). The stock must rise above ₹1,620 at expiry for the trade to be profitable.
Example B — Long Put: Bearish Speculation or Hedge
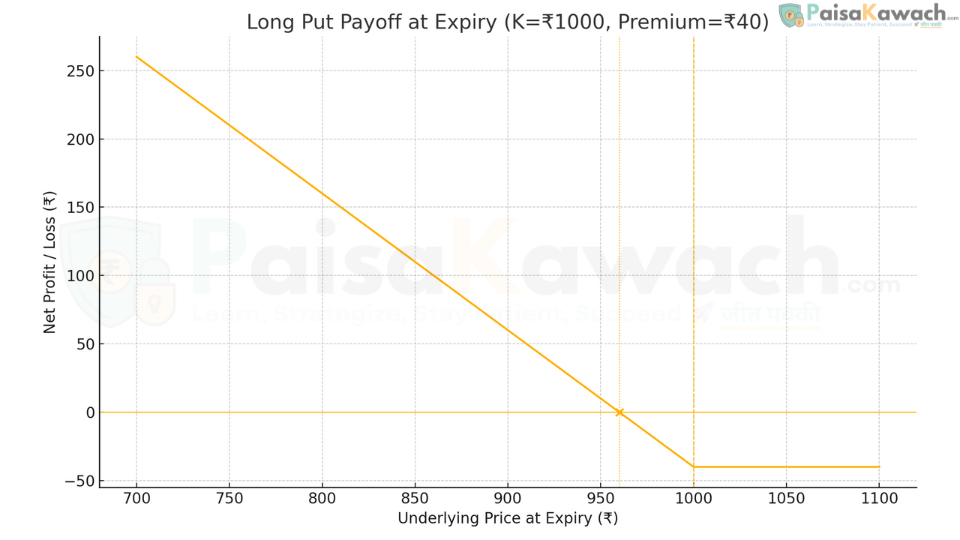
- Underlying: ABC Stock
- Strike Price (K): ₹1,000 (~$12.00)
- Premium Paid (P): ₹40 (~$0.48) per share
- Total Cost: ₹40 * 100 = ₹4,000 (~$48) (Max Loss)
Scenario 1: Expiry at ₹900 (Bear Case)
Intrinsic Value = max(0, 1000 - 900) = ₹100
Net Profit Per Share = ₹100 - ₹40 = ₹60 (~$0.72)
Total Net Profit = ₹60 * 100 = ₹6,000 (~$72)
Scenario 2: Expiry at ₹1,000 (Flat Case)
Intrinsic Value = max(0, 1000 - 1000) = ₹0
Net Loss Per Share = ₹0 - ₹40 = ₹40 (~$0.48) (Total Premium Lost)
Total Net Loss = ₹4,000 (~$48)
Scenario 3: Expiry at ₹1,100 (Bull Case)
Intrinsic Value = max(0, 1000 - 1100) = ₹0
Net Loss Per Share = ₹0 - ₹40 = ₹40 (~$0.48) (Total Premium Lost)
Total Net Loss = ₹4,000 (~$48)
Breakeven Point (BEP) = K - P = ₹1,000 - ₹40 = ₹960 (~$11.52). The stock must fall below ₹960 at expiry for the trade to be profitable.
5. Breakeven Analysis and Maximum Loss/Gain
- Long Call Breakeven:
BEP = Strike Price (K) + Premium Paid (P) - Long Put Breakeven:
BEP = Strike Price (K) - Premium Paid (P) - Maximum Loss (Buyer): Limited to the 100% of the premium paid (P). This occurs if the option expires Out-of-The-Money (OTM) or At-The-Money (ATM).
- Maximum Gain:
Long Call: Theoretically unlimited, as the underlying asset's price can rise indefinitely.
Long Put: Limited but substantial. The maximum profit occurs if the underlying asset's price falls to zero.Max Gain = (Strike Price (K) - 0) - Premium Paid (P).
6. Comparative Payoff Summary Table
| Position | Motivation | Maximum Profit | Maximum Loss | Breakeven at Expiry |
|---|---|---|---|---|
| Long Call | Bullish | Theoretically Unlimited | Premium Paid (P) | K + P |
| Short Call | Neutral/Bearish | Premium Received (P) | Theoretically Unlimited | K + P |
| Long Put | Bearish | K - P (if S=0) | Premium Paid (P) | K - P |
| Short Put | Neutral/Bullish | Premium Received (P) | K - P (if S=0) | K - P |
7. Practical Uses and Strategies
Protective Put (Portfolio Insurance)
Objective: To hedge against a decline in a stock you already own.
Example: You hold 100 shares of XYZ Ltd., purchased at ₹1,000 (~$12.00). You are concerned about short-term downside risk but don't want to sell. You buy one ATM Put option with a strike of ₹1,000 for a premium of ₹50 (~$0.60) per share (Total cost: ₹5,000 / ~$60).
Outcome: Your maximum loss on the shares is now capped. Even if XYZ falls to ₹800, your put option is worth ₹200 (₹1000 - ₹800), offsetting most of the ₹200 per share loss on the stock. Your net loss is reduced to the cost of the premium (₹50). This is analogous to paying an insurance premium.
Covered Call (Income Generation)
Objective: To generate income from a stock holding you believe will remain flat or rise slightly.
Example: You own 100 shares of RELIANCE, currently at ₹2,500 (~$30). You sell one OTM Call option with a strike of ₹2,600 and receive a premium of ₹80 (~$0.96) per share (Total credit: ₹8,000 / ~$96).
Outcome:
- If RELIANCE stays below ₹2,600 at expiry: The call expires worthless. You keep the ₹8,000 premium, enhancing your returns.
- If RELIANCE rises above ₹2,600: You are obligated to sell your shares at ₹2,600. You still keep the premium, so your effective selling price is ₹2,600 + ₹80 = ₹2,680 (~$32.16). You cap your upside but collect income.
Directional Speculation (Leveraged Bet)
Objective: To profit from a significant price move with limited capital outlay.
Example: You are bullish on INFY, trading at ₹1,800 (~$21.60). Instead of investing ₹180,000 to buy 100 shares, you buy one OTM Call option with a strike of ₹1,850 for a premium of ₹40 (~$0.48) per share (Total cost: ₹4,000 / ~$48).
Outcome: If INFY surges to ₹1,950, your call has an intrinsic value of ₹100. Your net profit is (₹100 - ₹40) * 100 = ₹6,000 (~$72), a 150% return on your premium. If you were wrong and the stock stays flat, your loss is limited to ₹4,000, far less than the loss from owning the stock if it had fallen.
8. Intrinsic Value vs. Extrinsic (Time) Value
- Intrinsic Value: The tangible, real value of an option if it were exercised immediately. It is never negative.
Call Intrinsic Value:max(0, Current S - K)
Put Intrinsic Value:max(0, K - Current S)
An option trading at or below its intrinsic value presents an arbitrage opportunity. - Extrinsic Value (Time Value): The portion of an option's premium that exceeds its intrinsic value. It is the "hope value" or "time value."
Extrinsic Value = Total Premium - Intrinsic Value
This value reflects:- Time to Expiration: More time = more opportunity for the option to become profitable = higher extrinsic value.
- Implied Volatility (IV): Higher expected future volatility = higher chance of a big move = higher extrinsic value.
- Interest Rates & Dividends: These have a smaller, more complex effect on extrinsic value.
Example: A Call option has a strike of ₹1,000. The underlying stock is at ₹1,050. The option trades for ₹70.
Intrinsic Value = ₹1,050 - ₹1,000 = ₹50
Extrinsic Value = ₹70 - ₹50 = ₹20
This ₹20 will decay to zero as the option approaches expiry, all else being equal.
9. Introduction to The "Greeks"
The "Greeks" are risk measures that quantify how an option's price is expected to change based on various factors. They are essential for advanced trading and risk management.
- Delta (Δ): Measures the sensitivity of an option's price to a ₹1 change in the price of the underlying asset. For example, a Delta of 0.50 means the option's price will change by approximately ₹0.50 for every ₹1 move in the stock. Calls have positive Delta; Puts have negative Delta.
- Gamma (Γ): Measures the rate of change of Delta relative to the underlying asset's price. It indicates how stable or unstable Delta is. High Gamma means Delta can change rapidly.
- Theta (Θ): Measures the sensitivity of an option's price to the passage of time (time decay). It is typically negative for option buyers, representing the daily erosion of extrinsic value. Theta accelerates as expiration nears.
- Vega (ν): Measures the sensitivity of an option's price to changes in the implied volatility of the underlying asset. A Vega of 0.10 means the option's price will change by ₹0.10 for every 1% change in implied volatility.
10. Critical Risk Controls & Practical Tips
- Position Sizing: Never risk more than a small percentage (e.g., 1-5%) of your total capital on any single options trade. The premium paid is your maximum loss—size accordingly.
- Define Your Exit: Before entering a trade, know your exit plan. At what underlying price will you take profits? At what point will you cut your losses? This is especially critical for short options.
- Respect Theta (Time Decay): As a buyer, time is your enemy. Avoid buying short-dated OTM options unless you expect an immediate, large move. As a seller, time is your friend.
- Monitor Implied Volatility (IV): Buy options when IV is relatively low (cheaper premiums). Sell options when IV is relatively high (more expensive premiums).
- Start Simple: Master long calls and long puts before venturing into more complex multi-leg strategies like spreads, straddles, and iron condors.
11. Summary
Calls and puts are the essential building blocks of the options market, offering defined risk for buyers and defined (but potentially large) reward for sellers. Mastery of their payoff profiles, breakeven points, and the concepts of intrinsic/extrinsic value is non-negotiable for any serious trader or investor. These instruments provide powerful and flexible tools for speculation, hedging, and income generation. Remember, the premium is the buyer's maximum loss and the seller's initial gain. In the next chapter, we will delve deeper into the Option Greeks—Delta, Gamma, Theta, and Vega—to understand the dynamic behavior of option prices.


