Option Greeks — Delta, Gamma, Theta, Vega, Rho (Practical Guide)

A focused study of option Greeks: delta, gamma, theta, vega, and rho — what they measure, how to read them, worked examples, and how traders use Greeks to manage risk.
Option Greeks are the essential quantitative risk measures that decode how an option's price is expected to react to changes in various market forces. They are the partial derivatives of the option pricing model and provide a dynamic lens through which traders can dissect and manage exposure to direction, time decay, volatility, and interest rates. A deep understanding of Greeks is what separates novice traders from sophisticated strategists, enabling precise hedging and risk assessment in both single options and complex multi-leg positions.
1. What Are the Greeks? — A Comprehensive Overview
Greeks are the mathematical heart of options pricing, representing the sensitivity of an option's premium to a single variable while holding all others constant. They transform abstract market movements into quantifiable risk metrics, allowing for scientific portfolio management.
- Delta (Δ): The first-order derivative measuring sensitivity to changes in the price of the underlying asset.
- Gamma (Γ): The second-order derivative, measuring the rate of change of Delta itself.
- Theta (Θ): The derivative measuring sensitivity to the passage of time (time decay).
- Vega (ν): The derivative measuring sensitivity to changes in the implied volatility (IV) of the underlying asset.
- Rho (ρ): The derivative measuring sensitivity to changes in the risk-free interest rate.
Each Greek provides a unique and critical insight into the non-linear behavior of option prices.
2. Delta (Δ) — The Directional Hedge

Delta is the most fundamental Greek, estimating the change in an option's price for a ₹1 change in the underlying asset's price. It is often interpreted as the approximate probability that an option will expire in-the-money.
- Range & Interpretation:
- Call Options: Range from 0.00 (far OTM) to 1.00 (deep ITM). A Delta of 0.60 suggests a ~60% chance of expiring ITM and that the option's price will move ₹0.60 for every ₹1.00 move in the underlying.
- Put Options: Range from 0.00 (far OTM) to -1.00 (deep ITM). A Delta of -0.40 means the option's price will move -₹0.40 for every ₹1.00 move in the underlying. - Hedge Ratio (Delta Hedging): Delta enables the creation of a market-neutral position. To hedge 1 long call option with a Delta of 0.75, one would short 75 shares of the underlying stock (assuming a standard lot size of 100). This neutralizes the directional risk from small price movements.
Detailed Example: You hold a NIFTY call option with a Delta of 0.45. If the NIFTY 50 index moves from 20,000 to 20,100 (a +100 point move), the option's price is expected to increase by approximately 100 points * 0.45 = ₹45.
3. Gamma (Γ) — The Accelerator of Delta
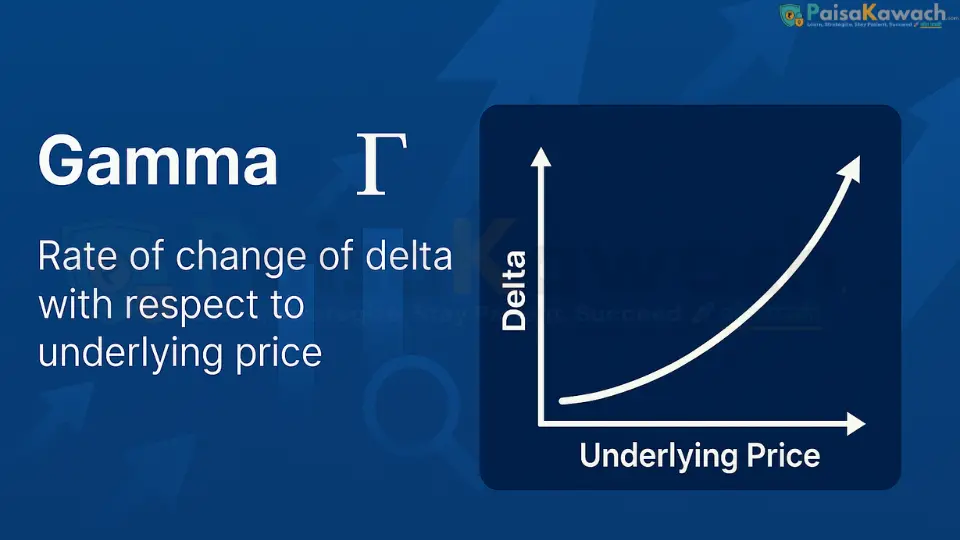
Gamma measures the rate of change of an option's Delta relative to a ₹1 change in the underlying asset. It is the second derivative of the option's price and reveals the "convexity" or "curvature" of an option's position. Gamma is highest for At-The-Money (ATM) options and increases as expiration approaches.
- Interpretation: A Gamma of 0.03 means that for a ₹1 increase in the underlying, the option's Delta will increase by 0.03. If the Delta was 0.50 and the underlying rises ₹10, the new Delta would be approximately 0.50 + (0.03 * 10) = 0.80.
- Long vs. Short Gamma:
- Long Options (Buyers): Are "long Gamma." This is beneficial as large price moves cause the position's Delta to move favorably (increases for calls, decreases for puts), accelerating profits.
- Short Options (Sellers): Are "short Gamma." This is dangerous as large price moves cause the position's Delta to move adversely, accelerating losses and forcing constant re-hedging.
Practical Implication: Market makers and delta hedgers must constantly monitor Gamma. A high-Gamma position requires frequent rebalancing of the hedge (buying high and selling low), which incurs significant transaction costs, especially in volatile markets.
4. Theta (Θ) — The Time Decay Clock
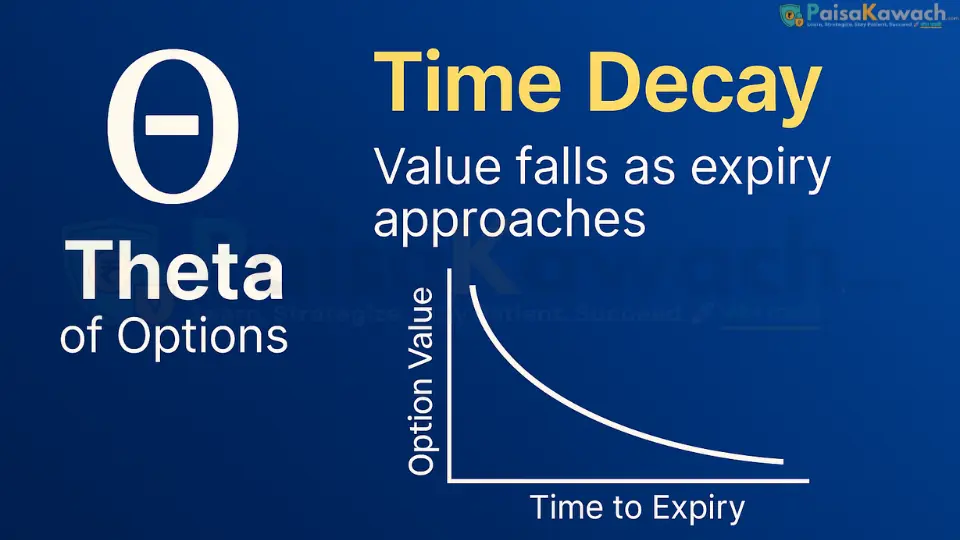
Theta quantifies the daily erosion of an option's extrinsic value due to the passage of time, assuming all other factors remain unchanged. It is often called "time decay." Theta is not linear; it accelerates dramatically in the final weeks and days before expiration.
- Interpretation: A Theta of -₹12.50 means the option will lose approximately ₹12.50 in value each passing day, purely from time decay.
- Impact on Positions:
- Option Buyers: Are "short theta" or "theta negative." Time decay is their enemy. They need a favorable price move to overcome this constant drain.
- Option Sellers: Are "long theta" or "theta positive." They profit from time decay, as the options they sold lose value each day, all else being equal.
Detailed Example: You buy a weekly ATM call option on Monday for a premium of ₹100. Its daily Theta is -₹20. By Friday, if the stock price and IV haven't changed, the option's value would have decayed by roughly ₹20 * 4 days = ₹80, leaving it worth only ~₹20. This illustrates the brutal effect of theta on short-dated options.
5. Vega (ν) — The Volatility Gauge
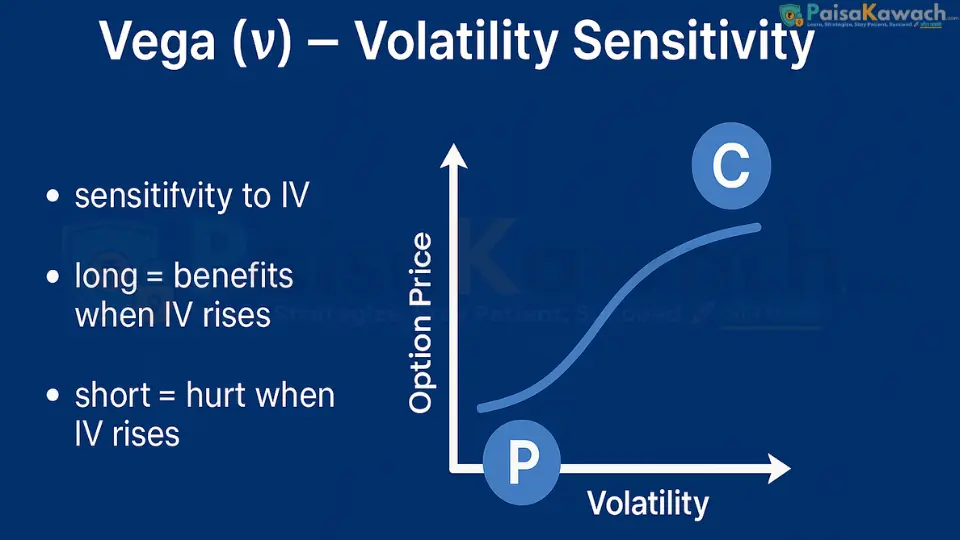
Vega measures an option's sensitivity to a 1% change in the implied volatility (IV) of the underlying asset. Implied volatility represents the market's forecast of future volatility. Vega is highest for ATM options with longer durations to expiration.
- Interpretation: A Vega of ₹0.25 means that for every 1% increase in IV, the option's price will increase by ₹0.25. A 5% increase in IV would add approximately ₹1.25 to the premium.
- Impact on Positions:
- Long Options (Buyers): Are "long vega." They benefit from increases in IV, which inflates the option's premium. This is why traders often buy options ahead of expected news events.
- Short Options (Sellers): Are "short vega." They are hurt by increases in IV, which increases the value of the liabilities they have sold.
Detailed Example: You are long a strangle (long OTM call and put) with a combined Vega of ₹50. If market uncertainty causes IV to spike from 20% to 25% (a +5% change), the value of your position would increase by approximately ₹50 * 5 = ₹250, even if the stock price hasn't moved yet.
6. Rho (ρ) — The Interest Rate Sensitivity
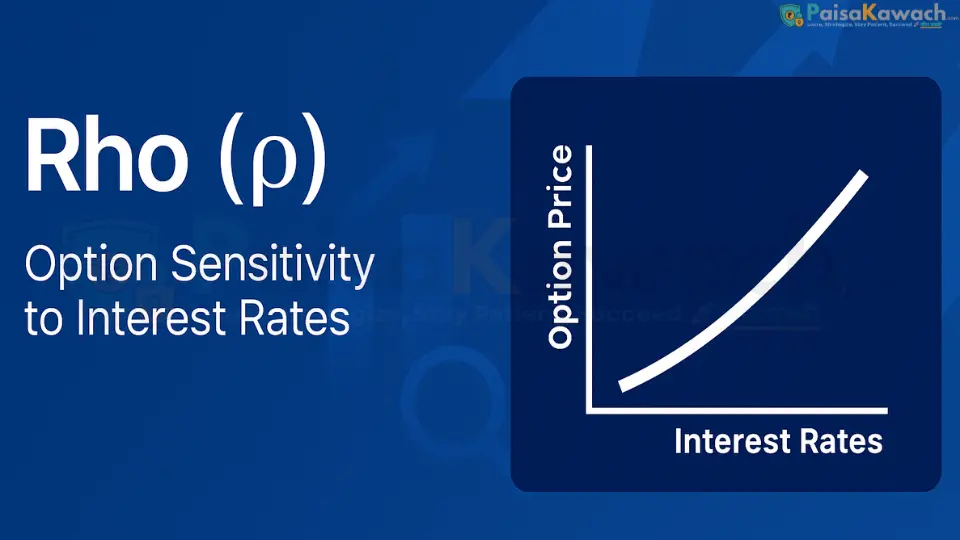
Rho measures the sensitivity of an option's price to a 1% change in the risk-free interest rate. Its effect is more pronounced on long-dated options (LEAPS) and is generally a secondary consideration for short-term equity option traders.
- Interpretation & Impact:
- Call Options: Have positive Rho. Rising interest rates increase the cost of carrying a short stock position, making calls slightly more attractive. A Rho of ₹0.60 means a 1% rate hike adds ₹0.60 to the call's price.
- Put Options: Have negative Rho. Rising rates make the protective put strategy slightly less attractive. A Rho of -₹0.40 means a 1% rate hike subtracts ₹0.40 from the put's price.
7. Greeks in Combination — Practical Trading Scenarios
Scenario A — The Delta-Gamma Hedging Dance
You are long 10 ATM call options on Stock XYZ. Each option has a Delta of 0.55 and a Gamma of 0.02. To delta-hedge, you short 550 shares of XYZ (0.55 * 10 contracts * 100 shares).
The Gamma Effect: If XYZ's stock price increases by ₹5, the Delta of your calls increases by (0.02 * 5) = 0.10, from 0.55 to 0.65 per option. Your total position Delta is now long (0.65 * 1000 shares) - 550 short shares = +100 shares. Your previously neutral hedge is now bullish. To re-hedge, you must short an additional 100 shares. This constant need to adjust the hedge is driven by Gamma.
Scenario B — The Vega-Theta Trade-Off
You buy a 30-day ATM straddle (long call and long put) to bet on an upcoming earnings announcement. This position is:
- Long Vega: You want IV to increase or stay high.
- Short Theta: You are paying significant time decay each day.
The Outcome: The company reports earnings, but the stock moves less than expected. Although IV collapses (hurting your Vega), the lack of a big price move means your options lose most of their value from Theta decay. This scenario highlights how a correct volatility forecast can be wiped out by incorrect timing or direction.
8. Greeks Across the Option Chain ("The Smile")
- At-The-Money (ATM) Options: Exhibit the highest Gamma and Theta. They also have the highest Vega sensitivity, making them the most reactive to changes in all variables.
- Out-of-The-Money (OTM) Options: Have low Delta and low Gamma. Their value is almost entirely extrinsic, so they have high Theta decay as a percentage of their premium. Their Vega is still significant if there is ample time to expiry.
- In-The-Money (ITM) Options: behave more like the underlying stock. Calls have Delta near +1, Puts have Delta near -1. They have low Gamma and lower sensitivity to Theta and Vega compared to ATM options.
9. Portfolio Greeks for Multi-Leg Strategies
Advanced traders manage the net Greeks of their entire portfolio. The Greeks of a multi-leg strategy are the sum of the Greeks of its individual legs.
- Credit Spread (e.g., Bull Put Spread): This strategy is typically net short Vega and net short Gamma (you want the stock to stay above a certain level). It is net positive Theta (you earn time decay) and has a defined net Delta (slightly bullish).
- Straddle/Strangle: As discussed, these are long Vega, long Gamma, and short Theta. They are approximately Delta-neutral when initiated ATM.
- Iron Butterfly: Designed to be Delta-neutral, short Vega, and short Gamma. It is a primarily Theta-positive (income) strategy that profits from low volatility and time decay.
10. Practical Risk Management Rules
- Dynamic Monitoring: Greeks are not static. Continuously monitor your portfolio's net Greeks as the underlying price moves, time passes, and volatility shifts.
- Hedging Cost Awareness: Delta-hedging a high-Gamma portfolio can be expensive due to frequent trading and bid-ask spreads. Ensure the strategy's edge outweighs these costs.
- Event Risk: Avoid being net short Gamma or net short Vega ahead of major scheduled events (e.g., earnings, Fed meetings), where large, unpredictable moves and volatility spikes can occur.
- Position Sizing: Size positions based on your portfolio's Greek exposure. For example, limit the total Vega exposure to a percentage of your capital to survive a sudden IV spike.
11. Quick Reference Summary Table
| Greek | Measures Sensitivity To | Long Call | Long Put | Primary Use |
|---|---|---|---|---|
| Delta (Δ) | Underlying Price | 0 to +1 | -1 to 0 | Directional Exposure & Hedging |
| Gamma (Γ) | Change in Delta | Positive | Positive | Convexity Risk & Hedge Rebalancing |
| Theta (Θ) | Time Decay | Negative | Negative | Income (Selling) / Risk (Buying) |
| Vega (ν) | Implied Volatility | Positive | Positive | Volatility Trading & Hedging |
| Rho (ρ) | Interest Rates | Positive | Negative | Long-Dated Option Valuation |
12. Summary
The Greeks provide a sophisticated framework for deconstructing option risk into its core components: Delta (direction), Gamma (acceleration), Theta (time), Vega (volatility), and Rho (rates). Mastering their interactions is paramount for effective trading and risk management. A successful options trader doesn't just predict price direction; they manage a dynamic portfolio of sensitivities, balancing the trade-offs between time decay, volatility exposure, and directional bias. In the next chapter, we will apply these concepts through worked calculations and explore the specific Greek profiles of popular multi-leg strategies.


